- 스티커 모으기(2)
문제 설명
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.
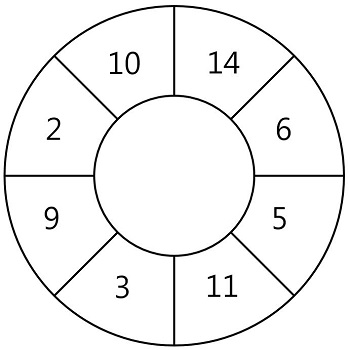
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.
제한 사항
- sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
- sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
- 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.
입출력 예
stickeranswer
| [14, 6, 5, 11, 3, 9, 2, 10] | 36 |
| [1, 3, 2, 5, 4] | 8 |
입출력 예 설명
입출력 예 #1
6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.
입출력 예 #2
3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.
https://programmers.co.kr/learn/courses/30/lessons/12971
코딩테스트 연습 - 스티커 모으기(2)
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다. 원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록
programmers.co.kr
def solution(sticker):
if len(sticker) <= 3:
return max(sticker)
answer = 0
# 첫 번째 선택
dp1 = [0 for _ in range(len(sticker))]
# 첫 번째 선택 x
dp2 = [0 for _ in range(len(sticker))]
dp1[0], dp1[1] = sticker[0], sticker[0]
dp2[0], dp2[1] = 0, sticker[1]
for i in range(2, len(sticker)):
if i == len(sticker)-1:
dp2[i] = max(dp2[i-1], sticker[i]+dp2[i-2])
else:
dp1[i] = max(dp1[i-1], sticker[i]+dp1[i-2])
dp2[i] = max(dp2[i-1], sticker[i]+dp2[i-2])
answer = max(dp1[len(dp1)-2], dp2[len(dp2)-1])
return answer
정확성 테스트
테스트 1 〉 통과 (0.00ms, 10.3MB)
테스트 2 〉 통과 (0.00ms, 10.3MB)
테스트 3 〉 통과 (0.01ms, 10.3MB)
테스트 4 〉 통과 (0.01ms, 10.3MB)
테스트 5 〉 통과 (0.01ms, 10.3MB)
테스트 6 〉 통과 (0.02ms, 10.3MB)
테스트 7 〉 통과 (0.69ms, 10.2MB)
테스트 8 〉 통과 (0.65ms, 10.3MB)
테스트 9 〉 통과 (0.70ms, 10.3MB)
테스트 10 〉 통과 (0.67ms, 10.3MB)
테스트 11 〉 통과 (0.67ms, 10.3MB)
테스트 12 〉 통과 (0.69ms, 10.3MB)
테스트 13 〉 통과 (0.65ms, 10.3MB)
테스트 14 〉 통과 (0.70ms, 10.3MB)
테스트 15 〉 통과 (0.66ms, 10.4MB)
테스트 16 〉 통과 (0.65ms, 10.3MB)
테스트 17 〉 통과 (0.69ms, 10.3MB)
테스트 18 〉 통과 (0.65ms, 10.3MB)
테스트 19 〉 통과 (0.68ms, 10.3MB)
테스트 20 〉 통과 (0.73ms, 10.3MB)
테스트 21 〉 통과 (0.68ms, 10.3MB)
테스트 22 〉 통과 (0.76ms, 10.2MB)
테스트 23 〉 통과 (0.65ms, 10.3MB)
테스트 24 〉 통과 (0.68ms, 10.2MB)
테스트 25 〉 통과 (0.72ms, 10.3MB)
테스트 26 〉 통과 (0.67ms, 10.2MB)
테스트 27 〉 통과 (0.64ms, 10.3MB)
테스트 28 〉 통과 (0.66ms, 10.3MB)
테스트 29 〉 통과 (1.32ms, 10.3MB)
테스트 30 〉 통과 (0.73ms, 10.3MB)
테스트 31 〉 통과 (0.66ms, 10.3MB)
테스트 32 〉 통과 (0.67ms, 10.3MB)
테스트 33 〉 통과 (0.00ms, 10.3MB)
효율성 테스트
테스트 1 〉 통과 (71.91ms, 16.6MB)
테스트 2 〉 통과 (70.83ms, 16.4MB)
테스트 3 〉 통과 (72.40ms, 16.5MB)
테스트 4 〉 통과 (65.01ms, 16MB)
후기
다이나믹프로그래밍 문제다. 프로그래머스-도둑질 문제와 같은 방식으로 해결하였다.
풀이
* 2가지 케이스로 나눈다. 1번째 케이스는 처음 스티커를 사용하는 케이스, 2번 케이스는 처음 스티커 사용 X
(1) 케이스별로 1케이스 - dp1, 2케이스 - dp2 배열을 생성한다. dp1은 초기화를 dp1[0]=자신스티커,dp1[1]=dp1[0] 을 해줘야 하며, dp2는 초기화를 dp2[0]=0 (선택안함), dp2[1]=자신스티커 로 해야한다.
(2) dp는 max(직전까지의 최댓값, 이전이전까지의 최댓값 + 자기자신 스티커)로 계산한다.
'코딩 테스트&알고리즘 > 프로그래머스 level 3' 카테고리의 다른 글
| [파이썬] 프로그래머스 - 위클리 챌린지 3주차 (0) | 2021.08.19 |
|---|---|
| [파이썬 python] 프로그래머스 - 풍선 터트리기 (0) | 2021.08.16 |
| [파이썬 python] 프로그래머스 - 매칭 점수 (0) | 2021.08.12 |
| [파이썬 python] 프로그래머스 - 숫자 게임 (0) | 2021.08.08 |
| [파이썬 python] 프로그래머스 - 기지국 설치 (0) | 2021.08.07 |



댓글